계절요소 추가한 시계열 선형 모델 SARIMAX 파이썬 (python)

 

SARIMAX는 ARIMA와 함께 시계열 데이터 분석할 때 사용하는 모델이다. 

기존의 ARIMAX 모형에서 계절성 패턴을 추가한 모델로 SARIMAX의 X는 외부 변수를 나타내는 eXogeneous의 줄임말로 학습과 예측에 포함시킬 수 있다

 

 

from statsmodels.tsa.statespace.sarimax import SARIMAX

 

주요파라미터

 

Parameter	Description
endog	관측된 시계열 데이터
exog	외부 변수 데이터
order	ARIMA의 p, d, q
seasonal_order	SARIMA의 seasonal component (P, D, Q)s
enforce_stationary	AR항이 stationary를 띠게 함 (default=TRUE)
enforce_invertibility	MA항이 stationary를 띠게 함 (default=False)

 

p는 과거 관측 갯수, d는 차분횟수, q는 오차갯수

 

모델링을 하기 위해서는 p, d, q뿐만 아니라 seasonal component인 P, D, Q 하이퍼 파라미터를 설정해줘야 한다. (여기서 s는 12개월이라는 뜻으로 12로 설정한다.)

이중 가장 낮은 AIC / BIC 값을 가지는 파라미터 조합을 선택해야 하는 데 grid search라고 한다. 

p,d,q,P,D,Q는 0에서 3 사이의 값을 가진다고 보면 된다.

->why?

---

AIC(Akaike's information Criterion)란?

 

일반적인 회귀분석에서 쓰이는 지표로 주어진 데이터 셋에 대한 모델의 상대적 품질을 평가하여

model selection할 때 참고한다.

 

AIC값은 낮을수록 좋다고 하는데 AIC는 최소의 정보 손실을 갖는 모델이 가장 적합한 모델로 선택하는 것으로

2k는 해당 모형에 패널티를 주기 위해 사용되는 파라미터 갯수(설명변수 갯수) 즉 설명변수에 따라 모형의 적합도에 차이가 난다는 의미로 설명변수의 수가 증가할수록 2k를 증가시켜 패널티를 부과한다.

2k의 증가할수록 AIC값이 증가하게 되는 것.

 

 

AIC = 2(log-likelihood) +2k

      = n log(σ^2) + 2k

 

• likelihood = σ^2:SSRn : 모형 적합도를 나타내는 척도 
• n: 표본의 크기
• k: 모형 파라미터의 갯수

---

BIC(bayes information Criteria)란?

 

AIC의 단점은 표본인 n의 크기가 커질 때 부정확해진다는 것

이를 보완한 지표가 BIC이다 

 

BIC = -2log(likelihood) + plog(n)

• p: 변수의 갯수

 

선형 회귀의 경우 AIC는 nlog(RSS/n) + 2p, BIC는 nlog(RSS/n) +plog(n)

 

결국 AIC, BIC를 최소화 한다는 뜻은 우도(likelihood)를 가장 크게 하는 동시에 변수 갯수는 가장 적은 최적의 모델(parsimonious & explainable)을 의미

 

BIC의 경우 변수가 많을 수록 AIC보다 더 페널티를 가하므로 AIC보다 BIC 참고

 

---

모델 fitting 확인 

 

Ljung-Box(L1)

잔차가 white noise를 따르는지 판단하는 테스트 

귀무가설: 잔차가 white noise를 따른다

p-value가 낮으면 white noise를 따르지 않고 시간대 별 잔차가 corrleated 되어 있는 것으로 판단

 

Jarque-Bera 

귀무가설 : 잔차가 normal distribution을 따른다

p-value가 낮으면 귀무가설 기각

 

Heteroskedasticity

각 시간대 별 잔차의 분산이 일정한지 보는 테스트

귀무가설:  잔차의 분산이 일정하다

p-value가 낮으면 귀무가설 기각

 

 

---

plot_diagnostic을 이용하여 fitting 되어 있음을 확인

 

 

---

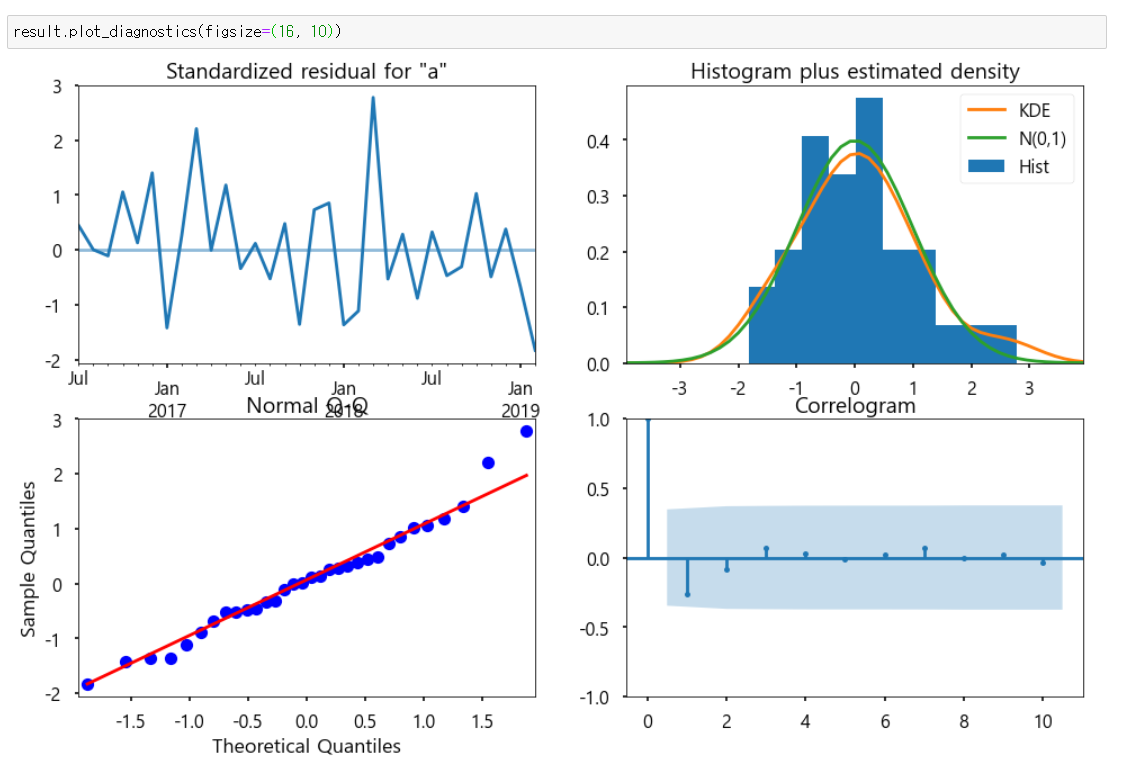
Prediction

 

get_prediction함수 사용, 예측할 기간의 start와 end 선택

 

pred = result.get_prediction(start=pd.to_datetime('2018-01-01'), end=pd.to_datetime('2019-02-28'), dynamic=True)

 

실제 funda 상점 월 매출 예측할 때는 월 갯수를 세서 선택했음, dynamic 파라미터가 True일 경우 학습 데이터 예측을 할 때 예측값 대신 실제값으로 이용하겠다는 뜻

 

 

 

---

이후 시점 예측 (prediction)하기

get_forecast(steps=n)함수로 샘플 바깥의 예측 수행할 수 있음

steps로 훈련에 사용한 데이터 바로 다음부터 지정한 step만큼 예측 가능

 

 

 

 

참고 블로그:

https://ehfgk78.github.io/2018/01/21/DataScience07TimeSeriesData01/

https://www.machinelearningplus.com/time-series/arima-model-time-series-forecasting-python/

https://h3imdallr.github.io/2017-08-19/arima/